山岳風景写真地理情報化パッケージ`alproj`の使い方
alprojの概要
alprojは山岳域で撮影された風景写真を地理情報化(いわゆるオルソ化)し、GISツールを用いた解析に用いることができるようにするPythonパッケージです。
これを既存の画像解析と組み合わせることによって、例えば登山者が撮影した風景写真から残雪域や植生の地図を作成することができます。
アルゴリズム
alprojは三つのステップを経て、風景写真の全画素に地理座標を与えます。
-
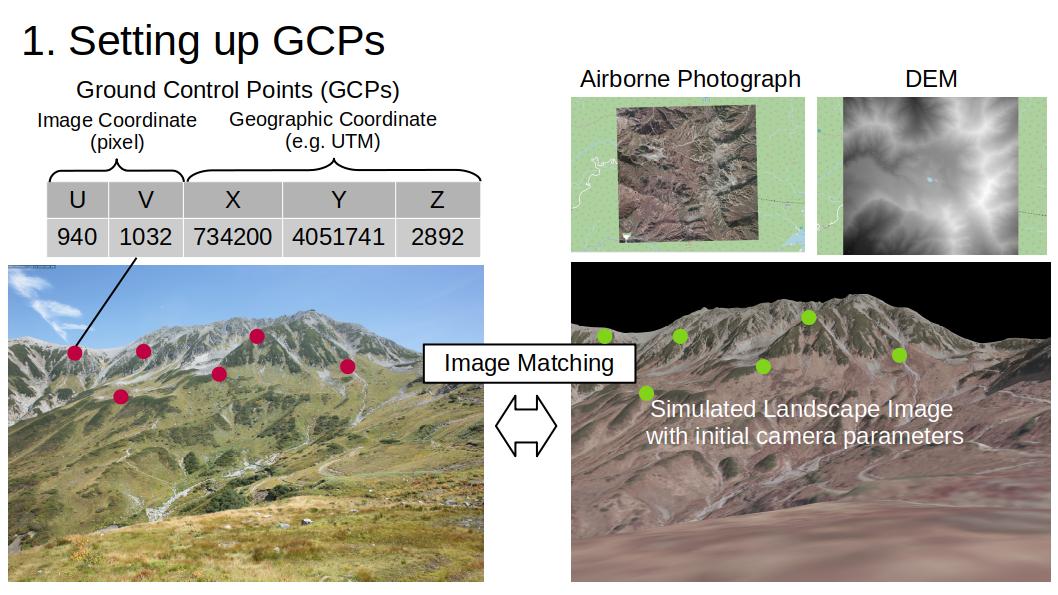
CGで作成した風景のシミュレーション画像(以下、シミュレーション画像)を用いて、写真中に地理座標のわかる点(Ground Control Points, GCPs)をみつける。
-
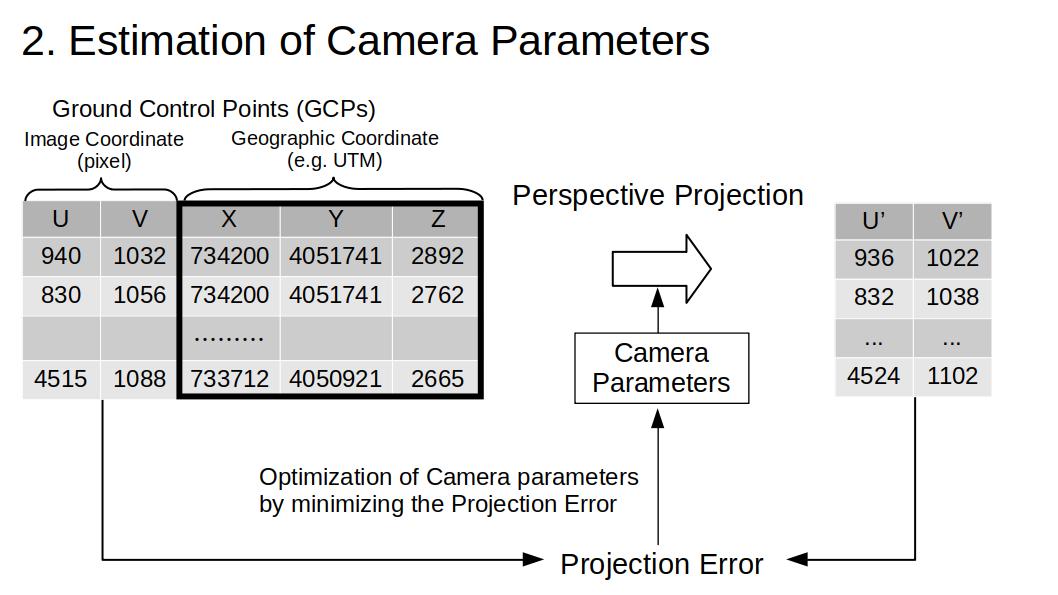
GCPを用いて風景写真のカメラパラメータ(カメラの向きやレンズの特性)を推定する。
-
推定されたカメラパラメータで写真を地形データ上に逆投影し、各画素に地理座標を紐付ける。
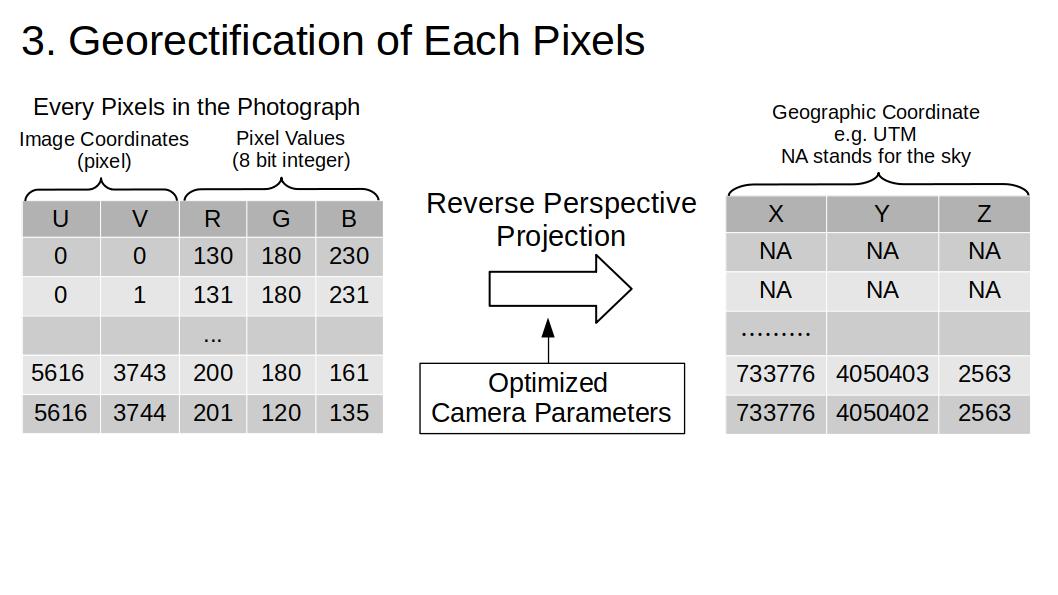
この結果、各画素が写している場所の地理座標が得られます。これをGISソフトに読み込ませることで、地理情報化の結果を視覚化することができます。

カメラモデル
alprojはOpenCVとほぼ同じカメラモデルを採用していますが、歪み係数を少しだけ変えています。
- OpenCV $$ \begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} x' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + 2 p_1 x' y' + p_2(r^2 + 2 x'^2) + s_1 r^2 + s_2 r^4 \\ y' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' + s_3 r^2 + s_4 r^4 \ \end{bmatrix} $$
- alproj $$ \begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} x' \frac{1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + k_4 r^2 + k_5 r^4 + k_6 r^6} + 2 p_1 x' y' + p_2(r^2 + 2 x'^2) + s_1 r^2 + s_2 r^4 \\ y' \frac{1 + a_1 + k_1 r^2 + k_2 r^4 + k_3 r^6}{1 + a_2 + k_4 r^2 + k_5 r^4 + k_6 r^6} + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' + s_3 r^2 + s_4 r^4 \ \end{bmatrix} $$
alprojでは画素のアスペクト比が1でない(画素が若干縦長や横長になっている)カメラを再現するために、a1、a2を追加しました。
動作環境
必要動作環境
- Python3
- RAM 12GB以上
- OpenGL(最近のPCであればまず大丈夫です) 試験した環境
- Ubuntu 20.04 LTS
- RAM 12 GB
- Python 3.8.5
依存パッケージ
alprojを使用するには以下のPythonパッケージが必要です。
numpy
pandas
datatable
rasterio
opencv-python
pillow
moderngl
cmaes
tqdm
インストール方法
alprojは以下でソースコードが公開されています。
https://github.com/0kam/alproj
pipを使ってインストールすることができます。
pip install git+https://github.com/0kam/alproj
使用例
ここでは国立環境研究所の立山定点撮影カメラ写真を例に、地理情報化の流れを説明します。写真は2016年に立山室堂山荘(富山県立山町)で撮影されたものです。以下ではこの写真をターゲット写真と呼びます。ターゲット写真の撮影位置は既知である必要があります。

事前に必要なデータ
alprojでの作業を始める前に、以下のデータを用意する必要があります。
-
オルソ済み航空写真

-
数値表層モデル(Digital Surface Model, DSM)

航空写真とDSMは
- ターゲット写真が写している領域をカバーし
- 同じ平面座標系(UTM座標系や平面直角座標系)に変換してある
必要があります。
必要なパッケージの読み込み
# Loading requirements
from alproj.surface import create_db, crop
from alproj.project import sim_image, reverse_proj
from alproj.gcp import akaze_match, set_gcp
from alproj.optimize import CMAOptimizer
import sqlite3
import numpy as np
import rasterio
①点群データベースの作成
まずはじめに、航空写真とDSMを用いて、当該山域の景観をCGで再現するための点群データベースを作成します。
res = 1.0 # 点群の平面解像度(m)
aerial = rasterio.open("airborne.tif") # 航空写真 例では40cm解像度のものを使いました。
dsm = rasterio.open("dsm.tif") # DSMここでは国土地理院のDEM5mを使っています。
out_path = "pointcloud.db" # 作成されるデータベースのパス
create_db(aerial, dsm, out_path) # 数分程度かかる場合があります。
これによって、以下の二つの要素を持ったSQLiteデータベースが作成されます。
-
vertices
点群の頂点データ
# x, y, zは頂点の座標、r, g, bは頂点の色を表します。 id x y z r g b 0 7.34942032e+05, 2.54030493e+03, 4.05319697e+06, 96, 91, 82 1 ... ... ... ... ... -
indices
頂点のインデックス
# それぞれの行はどの三つの頂点が一つの三角形を成すかを表します。 # 例えば一行目は、verticesの0, 3, 4行目の点が三角形を構成することを示しています。 v1 v2 v2 0 3 4 0 4 1 ... 7877845 7878552 7877846
②カメラパラメータの初期値の設定
カメラパラメータを推定するために、初期値を設定します。
- x, y, z
撮影位置の地理座標。撮影位置の推定はできません。はじめに設定した値がそのまま使われます。 - fov
視野角(度)。 - pan, tilt, roll
カメラ姿勢を表すオイラー角(度)。 - a1 ~ s4
歪み係数・ - w, h
画像の幅・高さ(ピクセル)。 - cx, cy
イメージセンサー上での主点の座標(ピクセル)。通常は中央(w/2, h/2)。
params = {"x":732731,"y":4051171, "z":2458, "fov":70, "pan":100, "tilt":0, "roll":0,\
"a1":1, "a2":1, "k1":0, "k2":0, "k3":0, "k4":0, "k5":0, "k6":0, \
"p1":0, "p2":0, "s1":0, "s2":0, "s3":0, "s4":0, \
"w":5616, "h":3744, "cx":5616/2, "cy":3744/2}
このカメラパラメータで景観のシミュレーション画像をレンダリングします。
まず、点群データベースからカメラから見える範囲の点群を取得します。
conn = sqlite3.connect("pointcloud.db")
distance = 3000 # The radius of the fan shape
chunksize = 1000000
vert, col, ind = crop(conn, params, distance, chunksize) # This takes some minutes.
以下のようなnp.arrayが得られます。
-
vert
頂点の地理座標。X, Z, Yの順番。
>>> vert array([[7.34942032e+05, 2.54030493e+03, 4.05319697e+06], [7.34943032e+05, 2.53846924e+03, 4.05319697e+06], [7.34941032e+05, 2.54056641e+03, 4.05319597e+06], ..., [7.34174032e+05, 2.15709058e+03, 4.04854197e+06], [7.34175032e+05, 2.15659692e+03, 4.04854197e+06], [7.34176032e+05, 2.15609204e+03, 4.04854197e+06]]) -
col
0〜1で表された各頂点の色。
>>> col array([[0.37647059, 0.35686275, 0.32156863], [0.36078431, 0.33333333, 0.30980392], [0.42352941, 0.40392157, 0.36078431], ..., [0. , 0. , 0. ], [0. , 0. , 0. ], [0. , 0. , 0. ]]) -
ind
どの三つの頂点が一つの三角形を成すかを示すインデックス。
>>> ind array([[ 0, 3, 4], [ 0, 4, 1], [ 1, 4, 5], ..., [7877844, 7878551, 7877845], [7877845, 7878551, 7878552], [7877845, 7878552, 7877846]], dtype=int64)
次に、シミュレーション画像をレンダリングします。
import cv2
sim = sim_image(vert, col, ind, params)
cv2.imwrite("devel_data/initial.png", sim)

シミュレーション画像は全画素が地理情報を持っているため、画像中の座標と地理座標の対応表を作成することができます。
df = reverse_proj(sim, vert, ind, params)
>>> df
u v x y z B G R
2058832 3376 366 734200.3125 4050691.75 2988.827881 116.0 120.0 124.0
2058833 3377 366 734199.6875 4050691.75 2988.624268 106.0 110.0 113.0
2058834 3378 366 734198.7500 4050691.25 2988.337402 82.0 86.0 88.0
2058835 3379 366 734198.0000 4050691.25 2988.081543 70.0 75.0 78.0
2058836 3380 366 734197.3750 4050691.25 2987.862061 60.0 65.0 68.0
... ... ... ... ... ... ... ... ...
21026299 5611 3743 732740.3125 4051161.75 2453.355469 113.0 117.0 148.0
21026300 5612 3743 732740.3125 4051161.75 2453.355469 113.0 117.0 148.0
21026301 5613 3743 732740.3125 4051161.75 2453.355713 113.0 117.0 148.0
21026302 5614 3743 732740.3125 4051161.75 2453.355713 113.0 117.0 148.0
21026303 5615 3743 732740.3125 4051161.75 2453.355713 113.0 117.0 148.0
[17336750 rows x 8 columns]
Ground Control Points (GCPs) の作成
シミュレーション画像と風景写真の間に対応点を見つけることで、風景写真中に地理座標と紐付いた点をいくつか作成します。画像間の対応点取得にはAKAZE 局所特徴量とFLANNを用いています。.
path_org = "target.jpg"
path_sim = "init.png"
match, plot = akaze_match(path_org, path_sim, ransac_th=200, plot_result=True)
cv2.imwrite("matched.png", plot)
gcps = set_gcp(match, df)
見つかった対応点。

>>> gcps
u v x y z
0 2585 1127 733720.2500 4051094.25 2648.573486
1 3566 631 734078.1250 4050727.00 2912.292969
2 3502 689 733951.8750 4050792.75 2849.661865
3 3745 723 733976.0625 4050697.25 2848.271729
4 3833 766 733996.1250 4050657.25 2841.155518
.. ... ... ... ... ...
147 3355 1126 733688.0625 4050916.50 2648.639893
148 4618 1190 733593.2500 4050619.00 2622.293457
149 2195 1243 733770.3750 4051216.00 2626.165527
150 2533 1777 733437.5625 4051142.25 2474.067383
151 3351 1072 733726.8750 4050907.00 2668.884766
uとvはそれぞれ、画像中のx軸方向、y軸方向の座標(左上原点)を表します。
カメラパラメータ推定
カメラパラメータは、GCPの地理座標を画像座標系に投影した際の再投影誤差を最小化することによって最適化されます。最適化にはCMA-ES を用いています。 最適化するカメラパラメータを選ぶこともできます。
obj_points = gcps[["x","y","z"]] # GCPの地理座標系での座標。Object points.
img_points = gcps[["u","v"]] # GCPの画像座標系での座標Image points.
params_init = params # カメラパラメータの初期値
target_params = ["fov", "pan", "tilt", "roll", "a1", "a2", "k1", "k2", "k3", "k4", "k5", "k6", "p1", "p2", "s1", "s2", "s3", "s4"] # 最適化するパラメータ。ここでは最適化できるもの全て。
cma_optimizer = CMAOptimizer(obj_points, img_points, params_init) # インスタンス生成.
cma_optimizer.set_target(target_params)
params_optim, error = cma_optimizer.optimize(generation = 300, bounds = None, sigma = 1.0, population_size=50) # 最適化の実行。errorが10ピクセル以下くらいまで下がらない場合は、繰り返し試してみてください。
>>> params_optim, error = cma_optimizer.optimize(generation = 300, bounds = None, sigma = 1.0, population_size=50)
100%|██████████████████████████████| 300/300 [00:34<00:00, 8.70it/s]
>>> error
4.8703777893270335
>>> params_optim
{'x': 732731, 'y': 4051171, 'z': 2458, 'w': 5616, 'h': 3744, 'cx': 2808.0, 'cy': 1872.0, 'fov': 72.7290644465022, 'pan': 96.61170204959896, 'tilt': -0.11552408078299625, 'roll': 0.13489679466899157, 'a1': -0.06632296375509533, 'a2': 0.017306226071500935, 'k1': -0.19848898326165829, 'k2': 0.054213972377095715, 'k3': 0.03875795616853486, 'k4': -0.08828147417948777, 'k5': -0.06425366365767886, 'k6': 0.05423288516486188, 'p1': 0.001605487393669105, 'p2': 0.0028034675418415864, 's1': -0.034626019251498615, 's2': 0.05211054664935553, 's3': 0.001925502186032381, 's4': -0.002550219390348231}
推定されたカメラパラメータでシミュレーション画像を作成すると、元の写真ときれいに重なることがわかります。
vert, col, ind = crop(conn, params_optim, 3000, 1000000)
sim2 = sim_image(vert, col, ind, params_optim)
cv2.imwrite("optimized.png", sim2)


最後に、風景写真の各画素が写している地理座標を得ることができます。 無事、風景写真の各画素にそれが写している場所の地理座標を付与することができました。
original = cv2.imread("ttym_2016.jpg")
georectificated = reverse_proj(original, vert, ind, params_optim)
>>> georectificated
u v x y z B G R
3047434 3562 542 734196.7500 4050689.00 2987.948242 176.0 160.0 148.0
3047435 3563 542 734194.6875 4050689.25 2987.231934 171.0 155.0 143.0
3047436 3564 542 734193.3125 4050689.25 2986.759521 175.0 159.0 146.0
3047437 3565 542 734192.6250 4050689.00 2986.516602 185.0 169.0 156.0
3047438 3566 542 734192.1250 4050688.75 2986.366943 191.0 179.0 161.0
... ... ... ... ... ... ... ... ...
21026299 5611 3743 732739.0000 4051163.50 2453.503174 98.0 153.0 156.0
21026300 5612 3743 732739.0000 4051163.50 2453.503174 92.0 151.0 153.0
21026301 5613 3743 732739.0000 4051163.50 2453.503174 88.0 152.0 153.0
21026302 5614 3743 732739.0000 4051163.50 2453.503418 89.0 153.0 157.0
21026303 5615 3743 732739.0000 4051163.50 2453.503418 89.0 156.0 159.0
[16456070 rows x 8 columns]
>>>
得られた結果は各画素を地理座標系に投影した際の点データです。GISツールを用いることでこの結果を可視化することができます。ここではRのsf及びstarsパッケージを用いて可視化を行います。.
library(sf)
library(stars)
library(tidyverse)
# Read result csv file
points <- read_csv(
"georectificated.csv",
col_types = cols_only(x = "d", y = "d", R = "d", G = "d", B = "d")
) %>%
mutate(R = as.integer(R), G = as.integer(G), B = as.integer(B))
# Converting the dataframe to points.
points <- points %>%
st_as_sf(coords = c("x", "y"))
# Rsaterize
R <- points %>%
select(R) %>%
st_rasterize(dx = 5, dy = 5)
G <- points %>%
select(G) %>%
st_rasterize(dx = 5, dy = 5)
B <- points %>%
select(B) %>%
st_rasterize(dx = 5, dy = 5)
rm(points)
gc()
raster <- c(R, G, B) %>%
merge() %>%
`st_crs<-`(6690)
# Plotting
ggplot() +
geom_stars(data = st_rgb(raster)) +
scale_fill_identity()
# Saving raster data as a GeoTiff file.
write_stars(raster, "ortholike.tif")
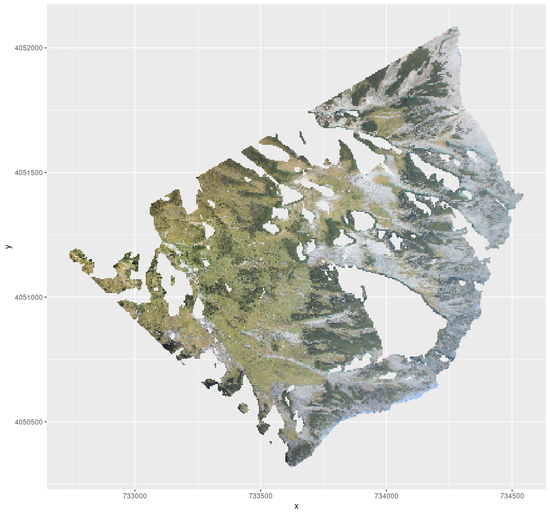
高山生態学、雪氷学への応用
ここでは写真のRGB値をそのまま用いましたが、 写真を残雪の有無や植生ごとに塗り分けた画像に変換した後にalprojを用いて地理座標を付与することで、残雪マップや植生図を得ることもできます。これによって、例えば山小屋設置のウェブカメラの画像等を用いて残雪や紅葉の様子を地理情報として取得し、他の地理情報と組み合わせて解析を行うことができるようになります!